Comprehensive Guide to Cos Values List: Understanding Cosine in Trigonometry

The cosine function, often abbreviated as cos, is a fundamental concept in trigonometry and mathematics. Understanding the cos values list is crucial for solving various problems in fields like physics, engineering, and computer graphics. This article provides a comprehensive overview of cosine values, their significance, and how they are applied in real-world scenarios. Whether you’re a student grappling with trigonometry or a professional needing a refresher, this guide aims to clarify and simplify the intricacies of the cos values list.

What is Cosine?

Cosine is one of the primary trigonometric functions, along with sine and tangent. In a right-angled triangle, the cosine of an angle is defined as the ratio of the length of the adjacent side to the length of the hypotenuse. Mathematically, it’s expressed as:

cos(θ) = Adjacent / Hypotenuse

Here, θ represents the angle in question. The cosine function is periodic, meaning its values repeat at regular intervals. This periodicity is a key characteristic that makes it useful in modeling oscillatory phenomena.

Understanding the Unit Circle

The unit circle is an essential tool for visualizing and understanding trigonometric functions, including cosine. It’s a circle with a radius of 1 centered at the origin (0,0) in a coordinate plane. As a point moves around the unit circle, its x-coordinate corresponds to the cosine of the angle formed between the positive x-axis and the line connecting the origin to that point. This visual representation helps in understanding how cos values list change as the angle varies from 0 to 360 degrees (or 0 to 2π radians).

Key Angles and Their Cosine Values

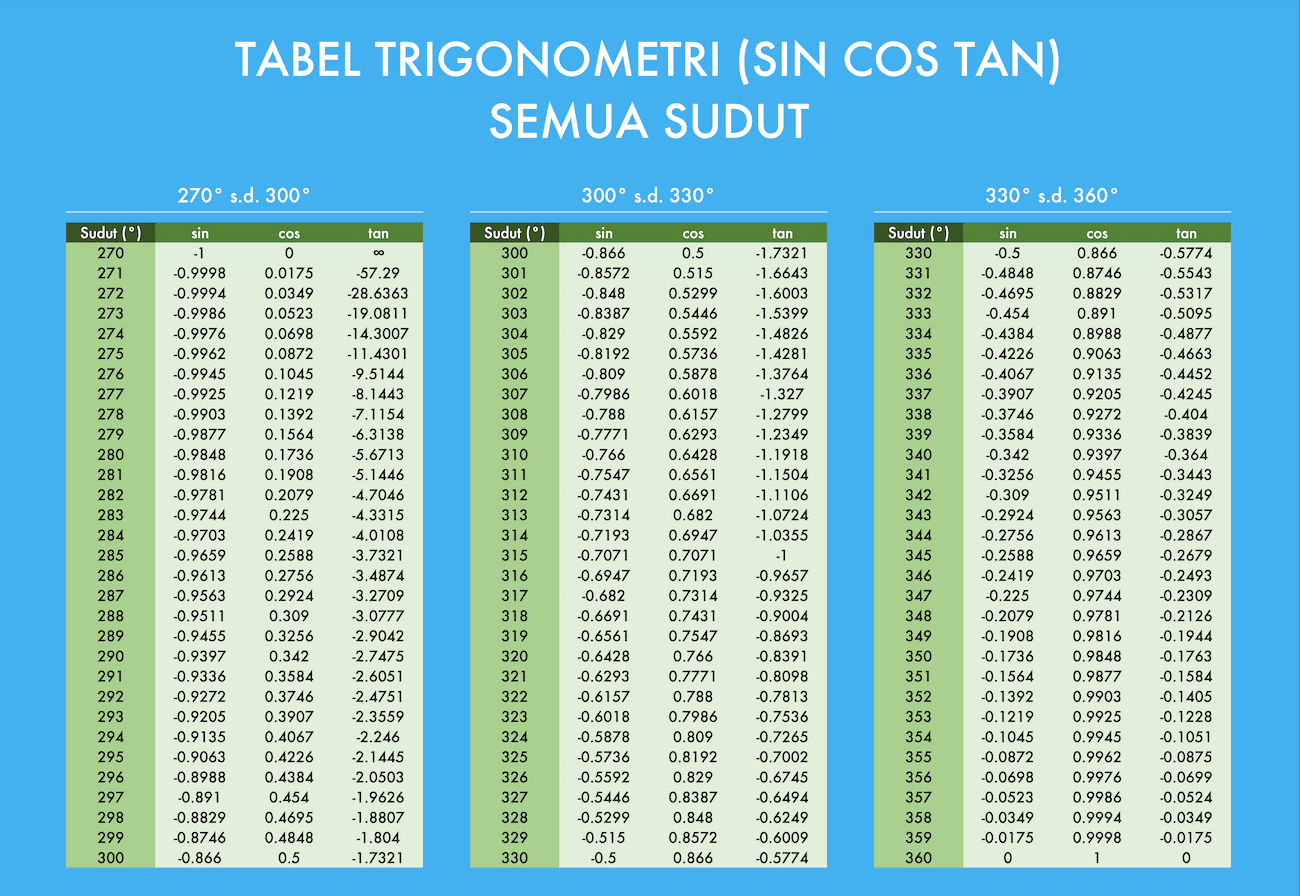
Certain angles appear frequently in trigonometric problems, and knowing their cosine values is extremely helpful. Here’s a list of some key angles and their corresponding cosine values:

0° (0 radians): cos(0°) = 1
30° (π/6 radians): cos(30°) = √3/2 ≈ 0.866
45° (π/4 radians): cos(45°) = √2/2 ≈ 0.707
60° (π/3 radians): cos(60°) = 1/2 = 0.5
90° (π/2 radians): cos(90°) = 0
120° (2π/3 radians): cos(120°) = -1/2 = -0.5
135° (3π/4 radians): cos(135°) = -√2/2 ≈ -0.707
150° (5π/6 radians): cos(150°) = -√3/2 ≈ -0.866
180° (π radians): cos(180°) = -1
210° (7π/6 radians): cos(210°) = -√3/2 ≈ -0.866
225° (5π/4 radians): cos(225°) = -√2/2 ≈ -0.707
240° (4π/3 radians): cos(240°) = -1/2 = -0.5
270° (3π/2 radians): cos(270°) = 0
300° (5π/3 radians): cos(300°) = 1/2 = 0.5
315° (7π/4 radians): cos(315°) = √2/2 ≈ 0.707
330° (11π/6 radians): cos(330°) = √3/2 ≈ 0.866
360° (2π radians): cos(360°) = 1

This cos values list is fundamental for quick calculations and understanding the behavior of the cosine function across different quadrants.

Properties of the Cosine Function

The cosine function has several important properties that are worth noting:

Domain: The domain of the cosine function is all real numbers.
Range: The range of the cosine function is [-1, 1]. This means that the cosine of any angle will always be between -1 and 1, inclusive.
Periodicity: The cosine function is periodic with a period of 2π (360°). This means that cos(θ) = cos(θ + 2πk) for any integer k.
Even Function: The cosine function is an even function, meaning that cos(-θ) = cos(θ). This symmetry about the y-axis is a useful property in many applications.

Applications of Cosine Values List

The cos values list and the cosine function, in general, have numerous applications across various fields:

Physics

In physics, cosine is used extensively in wave mechanics, optics, and mechanics. For example, when analyzing the motion of a pendulum, the cosine function describes the horizontal displacement of the pendulum bob as a function of time. Similarly, in alternating current (AC) circuits, voltage and current are often modeled using cosine functions.

Engineering

Engineers use cosine in structural analysis, signal processing, and control systems. In structural engineering, cosine is used to calculate the components of forces acting on a structure. In signal processing, cosine transforms are used to analyze and manipulate signals. [See also: Fourier Transform Explained]

Computer Graphics

In computer graphics, cosine is used for lighting calculations, rotations, and projections. The cosine of the angle between a light source and a surface determines the intensity of light reflected from that surface. Rotations in 2D and 3D space are also often represented using cosine and sine functions.

Navigation

Cosine is used in navigation for calculating distances and bearings. For example, the law of cosines is used to find the distance between two points on the Earth’s surface given their latitudes and longitudes.

Sound Engineering

When working with sound waves, cos values list and the cosine function are essential. Sound waves can be mathematically represented using trigonometric functions, and understanding the cosine values helps in analyzing and manipulating these waves for audio processing and synthesis. [See also: Understanding Sound Waves]

How to Calculate Cosine Values

While knowing the cosine values for key angles is helpful, there are situations where you need to calculate the cosine of an arbitrary angle. Here are a few methods for doing so:

Using a Calculator

The simplest way to find the cosine of an angle is to use a scientific calculator. Make sure the calculator is in the correct mode (degrees or radians) depending on the unit of the angle you’re working with. Simply enter the angle and press the cosine button.

Using Trigonometric Identities

Trigonometric identities can be used to express the cosine of an angle in terms of other trigonometric functions or angles. For example, the angle sum and difference identities can be used to find the cosine of angles that are sums or differences of known angles:

cos(A + B) = cos(A)cos(B) – sin(A)sin(B)
cos(A – B) = cos(A)cos(B) + sin(A)sin(B)

Using Series Expansions

The cosine function can be represented as an infinite series:

cos(x) = 1 – x²/2! + x⁴/4! – x⁶/6! + …

This series can be used to approximate the cosine of an angle, especially for small angles. However, for accurate results, a large number of terms may be needed.

Tips for Remembering Cosine Values

Remembering the cos values list can be challenging, but there are some tricks to make it easier:

Use the Unit Circle: Visualizing the unit circle can help you remember the cosine values for key angles. The x-coordinate of a point on the unit circle corresponds to the cosine of the angle.
Recognize Patterns: Notice the patterns in the cosine values for angles in different quadrants. For example, the cosine is positive in the first and fourth quadrants and negative in the second and third quadrants.
Use Mnemonics: Create mnemonic devices to remember the cosine values. For example, you could use a sentence or phrase where the first letter of each word corresponds to a key angle or value.
Practice: The more you practice using cosine values in problems, the easier it will be to remember them.

Common Mistakes to Avoid

When working with cosine values, it’s important to avoid common mistakes:

Incorrect Calculator Mode: Make sure your calculator is in the correct mode (degrees or radians) before calculating cosine values.
Sign Errors: Pay attention to the sign of the cosine value, especially in different quadrants.
Confusing Sine and Cosine: Remember that cosine is the ratio of the adjacent side to the hypotenuse, while sine is the ratio of the opposite side to the hypotenuse.

Advanced Topics Related to Cosine

Once you have a good understanding of the basics of cosine, you can explore more advanced topics:

Inverse Cosine Function (arccos): The inverse cosine function, also known as arccos or cos⁻¹, gives the angle whose cosine is a given value.
Hyperbolic Cosine (cosh): The hyperbolic cosine is a function defined in terms of exponential functions: cosh(x) = (eˣ + e⁻ˣ)/2.
Cosine Transform: The cosine transform is a mathematical transform that decomposes a function into a sum of cosine functions.

Conclusion

Understanding the cos values list and the cosine function is crucial for success in mathematics, physics, engineering, and many other fields. By mastering the concepts discussed in this article, you’ll be well-equipped to tackle a wide range of problems involving trigonometry. Remember to practice regularly and use the unit circle as a visual aid to reinforce your understanding. The cos values list is a powerful tool when understood and applied correctly. Whether you are calculating angles, analyzing waveforms, or designing structures, a solid grasp of cosine is essential.