Table of Contents

Understanding Cos Values: A Comprehensive List and Guide

In mathematics, particularly trigonometry, the cosine function, often abbreviated as cos, is a fundamental concept. It represents the ratio of the adjacent side to the hypotenuse in a right-angled triangle. The cos values list is a crucial tool for students, engineers, and professionals working with angles and their properties. This article aims to provide a comprehensive understanding of cos values, their significance, and a detailed cos values list for commonly used angles. Understanding these cos values is essential for various applications ranging from physics and engineering to computer graphics and navigation.

What is Cosine?

Before diving into the cos values list, let’s briefly recap what the cosine function entails. The cosine of an angle θ (theta) in a right-angled triangle is defined as:

cos(θ) = (Adjacent Side) / (Hypotenuse)

The cosine function is periodic with a period of 2π radians or 360 degrees. This means that cos(θ) = cos(θ + 2πk) for any integer k. Understanding this periodicity is crucial when dealing with angles beyond the standard range of 0 to 2π.

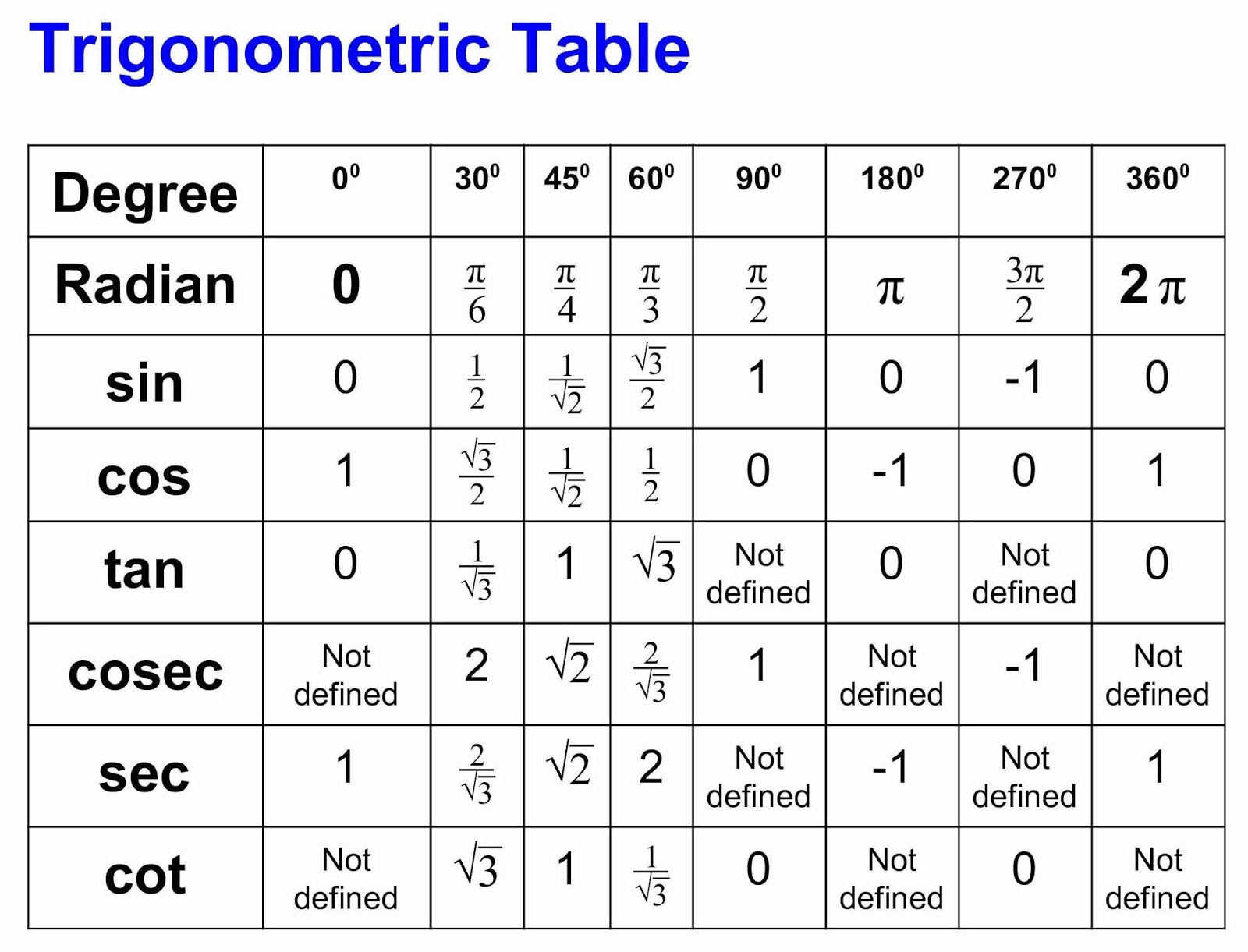
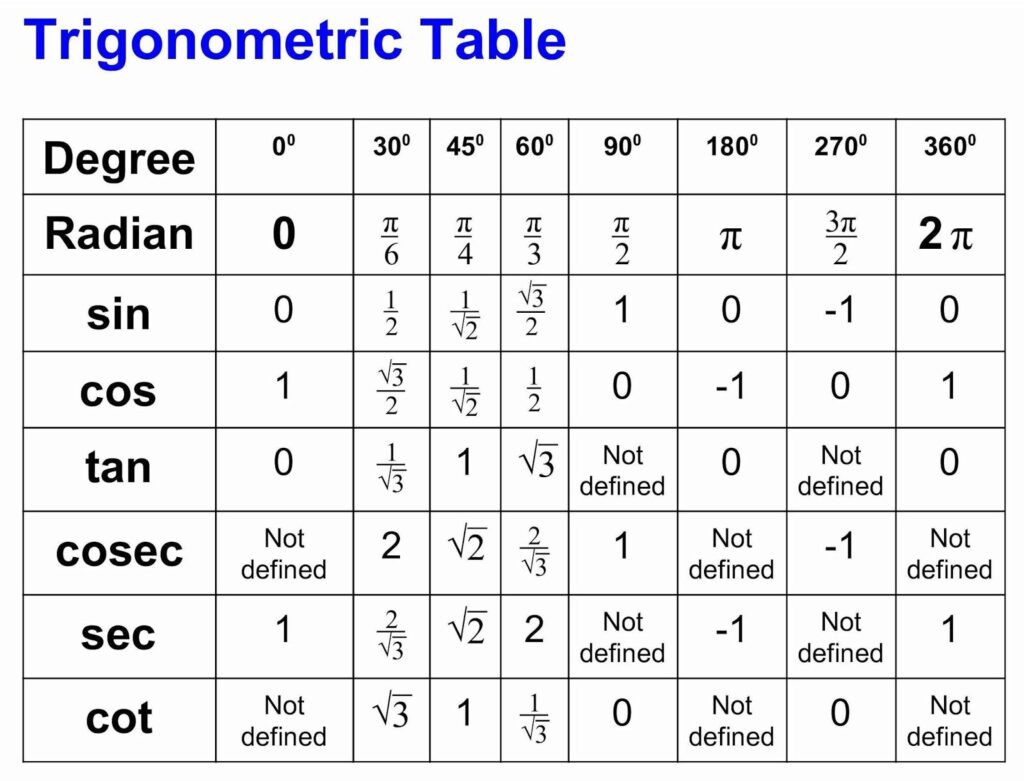
Common Angles and Their Cos Values: The Cos Values List

Certain angles appear frequently in mathematical and scientific contexts. Therefore, knowing the cosine values for these angles is highly beneficial. Here’s a cos values list for common angles:

0 degrees (0 radians): cos(0) = 1
30 degrees (π/6 radians): cos(π/6) = √3/2 ≈ 0.866
45 degrees (π/4 radians): cos(π/4) = √2/2 ≈ 0.707
60 degrees (π/3 radians): cos(π/3) = 1/2 = 0.5
90 degrees (π/2 radians): cos(π/2) = 0
120 degrees (2π/3 radians): cos(2π/3) = -1/2 = -0.5
135 degrees (3π/4 radians): cos(3π/4) = -√2/2 ≈ -0.707
150 degrees (5π/6 radians): cos(5π/6) = -√3/2 ≈ -0.866
180 degrees (π radians): cos(π) = -1
210 degrees (7π/6 radians): cos(7π/6) = -√3/2 ≈ -0.866
225 degrees (5π/4 radians): cos(5π/4) = -√2/2 ≈ -0.707
240 degrees (4π/3 radians): cos(4π/3) = -1/2 = -0.5
270 degrees (3π/2 radians): cos(3π/2) = 0
300 degrees (5π/3 radians): cos(5π/3) = 1/2 = 0.5
315 degrees (7π/4 radians): cos(7π/4) = √2/2 ≈ 0.707
330 degrees (11π/6 radians): cos(11π/6) = √3/2 ≈ 0.866
360 degrees (2π radians): cos(2π) = 1

This cos values list provides a quick reference for the cosine values of frequently encountered angles. Remembering these values can significantly speed up calculations and problem-solving in various fields.

The Unit Circle and Cosine

The unit circle is an invaluable tool for visualizing trigonometric functions. It’s a circle with a radius of 1 centered at the origin (0,0) in the Cartesian plane. The cosine of an angle θ is represented by the x-coordinate of the point where the terminal side of the angle intersects the unit circle.

Using the unit circle, you can easily determine the cosine values for any angle. Angles in the first quadrant (0 to 90 degrees) have positive cosine values, as their x-coordinates are positive. Angles in the second and third quadrants (90 to 270 degrees) have negative cosine values, and angles in the fourth quadrant (270 to 360 degrees) have positive cosine values again. This understanding helps in predicting the sign of the cos values.

Applications of Cosine Values

Cos values are not just abstract mathematical concepts; they have numerous practical applications across various disciplines:

Physics: In mechanics, cosine is used to resolve forces into components. For example, if a force is applied at an angle to a surface, the component of the force acting parallel to the surface is calculated using the cosine of the angle.
Engineering: Engineers use cosine in structural analysis to determine the stresses and strains in buildings and bridges. The cosine function helps in calculating the horizontal and vertical components of loads.
Navigation: Cosine is essential in GPS (Global Positioning System) and other navigation systems. It helps in calculating distances and directions based on angles and coordinates.
Computer Graphics: In computer graphics, cosine is used to calculate lighting effects and shading. It determines how light reflects off surfaces based on the angle of incidence.
Signal Processing: Cosine functions are fundamental in signal processing, especially in Fourier analysis, which decomposes signals into their constituent frequencies.
Electrical Engineering: In AC circuit analysis, cosine functions are used to represent alternating currents and voltages.

How to Calculate Cosine Values

While the cos values list provides values for common angles, you might need to calculate the cosine of other angles. Here are a few methods:

Calculators: Scientific calculators have built-in cosine functions. Ensure your calculator is set to the correct mode (degrees or radians) before calculating.
Programming Languages: Most programming languages, such as Python, Java, and C++, have built-in math libraries that include cosine functions.
Online Tools: Numerous online calculators and tools can compute cosine values for any angle.
Trigonometric Identities: You can use trigonometric identities to find cosine values for certain angles based on known values. For example, the half-angle formula can be used to find cos(θ/2) if you know cos(θ).

Understanding the Cosine Function’s Properties

To fully grasp the significance of cos values, it’s important to understand the properties of the cosine function:

Domain: The domain of the cosine function is all real numbers. You can input any angle (in degrees or radians) into the cosine function.
Range: The range of the cosine function is [-1, 1]. The cosine value always falls between -1 and 1, inclusive.
Periodicity: As mentioned earlier, the cosine function is periodic with a period of 2π (360 degrees).
Even Function: Cosine is an even function, meaning that cos(-θ) = cos(θ). This symmetry about the y-axis is an important property.
Zeros: The cosine function has zeros at odd multiples of π/2 (90 degrees). That is, cos(θ) = 0 when θ = (2n+1)π/2, where n is an integer.

Advanced Concepts Related to Cosine

For those seeking a deeper understanding, here are some advanced concepts related to the cosine function:

Taylor Series Expansion: The cosine function can be represented as an infinite series using the Taylor series expansion: cos(x) = 1 – (x^2)/2! + (x^4)/4! – (x^6)/6! + … This expansion is useful for approximating cosine values for small angles.
Complex Numbers: In complex analysis, the cosine function is related to the exponential function through Euler’s formula: e^(ix) = cos(x) + i sin(x). This connection is fundamental in many areas of mathematics and physics.
Fourier Transforms: Cosine functions are integral to Fourier transforms, which are used to analyze signals in the frequency domain. The cosine transform is a specific type of Fourier transform that decomposes a signal into cosine waves.

Tips for Remembering Cosine Values

Memorizing the cos values list can be challenging, but here are some tips to help:

Use the Unit Circle: Visualize the unit circle and remember that cosine corresponds to the x-coordinate.
Recognize Patterns: Notice the patterns in the cosine values for common angles. For example, cosine values decrease as you move from 0 to 90 degrees.
Mnemonics: Create mnemonic devices to remember the values. For example, you could create a sentence where each word’s length corresponds to a digit in the cosine value.
Practice: Regularly practice using cosine values in problems. The more you use them, the easier they will be to remember.
Flashcards: Use flashcards to quiz yourself on the cosine values of different angles.

Common Mistakes to Avoid

When working with cosine values, avoid these common mistakes:

Incorrect Mode: Ensure your calculator is in the correct mode (degrees or radians). Using the wrong mode will result in incorrect cosine values.
Sign Errors: Pay attention to the quadrant in which the angle lies. Cosine values are positive in the first and fourth quadrants and negative in the second and third quadrants.
Forgetting Periodicity: Remember that the cosine function is periodic. When dealing with angles outside the range of 0 to 360 degrees, adjust the angle accordingly.
Misunderstanding the Unit Circle: Ensure you understand that cosine corresponds to the x-coordinate on the unit circle.

Conclusion

The cos values list is a fundamental tool in mathematics and science, with applications spanning physics, engineering, computer graphics, and more. Understanding the properties of the cosine function, its relationship to the unit circle, and the values for common angles is crucial for success in these fields. By using the techniques and tips outlined in this article, you can master the cosine function and its applications. Whether you’re a student, engineer, or researcher, a solid understanding of cos values will undoubtedly prove invaluable.

From understanding the basics to exploring advanced concepts, this guide aims to provide a comprehensive overview of cos values, ensuring that you are well-equipped to tackle any problem involving cosine. Remember to practice regularly and utilize the resources available to enhance your understanding and proficiency.

[See also: Trigonometric Functions Explained]

[See also: Understanding Sine Values]